Parker Dimensional Analysis
A couple years ago, there was an interesting clip on MSNBC.
A few weeks later, Matt Parker came out with a video analyzing why people tend to make mistakes like this. Now I'm normally a huge fan of Matt Parker. But in this case, I think he kinda dropped the ball.
He does have a very good insight. He realizes that people are treating the "million" as a unit, removing it from the numbers before performing the calculation, then putting it back on at the end. This is indeed the proximate cause of the error. But Matt goes on to claim that the mistake is the treating of "million" as a unit; the implication being that, as a number suffix or a multiplier or however you want to think of it, it's not a unit, and therefore cannot be treated like one. This is false.
So what is a unit, really? When we think of the term, we probably think of things like "meters", "degrees Celcius", "watts", etc.; sciency stuff. But I think the main reason we think of those is due to unit conversion; when you have to convert from meters to feet, or derive a force from mass and acceleration, this makes us very aware of the units being used, and we associate the concept of "unit" with this sort of physics conversion.
In reality, a unit is just "what kind of thing you're counting". Matt uses two other examples in his video: "dollars" and "sheep". If I say "50 meters", that's just applying the number "50" to the thing "meters", saying that you have 50 of that thing. "50 sheep" works exactly the same way.
So what about "millions"? Well, we can definitely count millions! 1 million, 2 million, etc. You could imagine making physical groupings of a million sheep at a time, perhaps using some very large rubber bands, and then counting up individual clusters. "Millions" is a unit.
So if millions is a perfectly valid unit, why do we get an incorrect result if we take it off and then put it back on again after the calculation? Well, because you can't do that with other units either! 100 watts divided by 20 watts does not equal 5 watts. It equals the number 5, with no unit.
This is a somewhat subtle distinction, and easy to miss in a casual conversation. But it makes sense when you think about the actual things you're counting. 50 sheep is certainly not the same thing as 50 horses. And 50 sheep is also not the same thing as the abstract number 50; one is a group of animals, the other a mathematical concept. If someone were to say something to you involving the number 50, you would not simply assume that they're talking about sheep.
This perfectly solves the problem. If 100 watts / 20 watts equals only the number 5, with no "watts", then 100 million / 20 million equals only the number 5, with no "million".
But what about Matt's example? 80 million sheep - 50 million sheep = 30 million sheep; not just 30. That's because this is subtraction, not division. Units work differently depending on what operation you're performing! If you're doing addition or subtraction, the units are preserved; you can take them off at the beginning and then put them back on at the end. But for multiplication and division, this is not the case. Division cancels out the units, removing them entirely, and multiplication gives you a new unit, equal to the previous unit squared.
This seems kind of arbitrary, right? Why do they work differently depending on the operation? To understand this, let's go back to a different example that Matt used in his video. Near the beginning, when he's performing the division of $500 million / 327 million, he moves the dollar sign off to the left, then puts it back on afterwards to get the correct answer of $1.529. Why did that work? Didn't I just say that you can't do that for division?
The difference is in the units of the denominator. If the top and bottom of the fraction are both in the same unit, that unit cancels out and the resulting answer is just a number - referred to as "dimensionless". But in that calculation, the numerator was in dollars, but the denominator was dimensionless. There's nothing to cancel out, so the resulting number is still in dollars.
Think about what it means to multiply "5 sheep" by 2. You start with a row of 5 sheep. Then you take another of those rows and put it next to the first, such that you have 2 rows. Count up the sheep, and you get 10. So 5 sheep * 2 = 10 sheep. But what if you multiply 5 sheep by 2 sheep? We can start with the same thing, a row of 5 sheep. Now I need to take "2 sheep" many rows. What is a "sheep's worth" of rows? Nobody knows. It's a meaningless concept. If you really wanted to do this calculation, you'd just keep the units unmultiplied and report that as the answer, saying "10 sheep2". But really, if you ever find yourself doing a calculation like this, you should take that as a hint that something has gone wrong.
But not all units are meaningless when multiplied together. A million times a million is a trillion; a perfectly useful new unit. More abstract but still very useful: force = mass times acceleration. And of course it always makes sense to divide a unit by itself; if you try to divide some number of sheep by some other number of sheep, your answer is going to be in "sheep per sheep". Anything divided by itself is 1, and since multiplication by 1 always returns the same number you started with, we can ignore this.
So what a unit is is really just something you're multiplying by. "5 sheep" is the number 5 times the concept of sheep.
This sort of doing math with units and getting different units out is called dimensional analysis, and it can be tricky. One of my favorite examples is that if you think about how efficient your car is, you might phrase that in gallons of gas used per mile driven. But gallons is a unit of volume, which is length3, and mile is a unit of distance, or length. But anything cubed divided by itself is just itself squared. So car efficiency is measured in square length, also known as area. This seems weird at first, but unlike the earlier "square sheep", this actually has a very intuitive physical meaning; if you were to lay out the gas you burn in a tube on your route, the cross sectional area of that tube is equal to your car's efficiency in area. The less efficient your car is, the thicker the tube, meaning more gas is being burned per distance driven.
Dimensional analysis can get complicated, but I think learning the basics is worth it. Knowing that you preserve units when you add or subtract two numbers of the same unit, but you remove the units when you divide them, is very helpful, as it helps you avoid making mistakes like the one above.
It can also help with other kinds of mistakes. Take this tweet that was going around a while back:
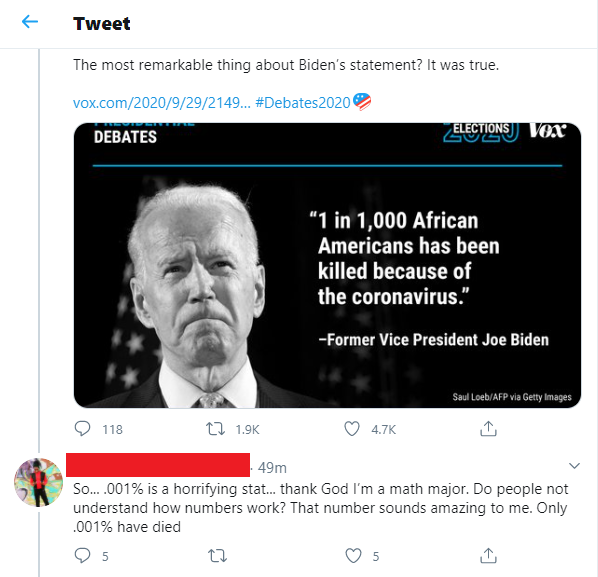
What this person seems to have done is thought to themselves "I want this number as a percentage", so they divided 1 by 1000 and then popped the percent sign on at the end.
This is easy to do, but uh... that's not how this works. That's not how any of this works. Units mean something. If the original numbers were dimensionless, the resulting answer isn't going to magically be of the unit "percent".
How do we convert an arbitrary quantity into another quantity of a desired unit? Well if you recall above, for a number to be "of" a unit means that the number is being multiplied by that unit. "10 sheep" means "sheep" times "the number 10". Doing some simple algebra, if you start with a quantity X and you want to represent that in the form N * Y, where Y is some preset constant, you derive N by dividing X by Y.
The input number is 0.001, so the result as a percentage is "(0.001/%)%". We can them simplify this by remembering that the definition of a percent is just the number 1/100. Calculating 0.001/(1/100) gives us 0.1, so the final answer is 0.1%.
The most fascinating unit conversion mistake I'm aware of was made by Verison in 2006. They quoted a price of 0.002 cents per kilobyte of data, and then charged 0.002 dollars per kilobyte.
What I found remarkable about this error was its persistence. In the MSNBC and Covid examples above, someone make a mistake, but once it was pointed out, they went "oops, ok I see where I went wrong".
There are a few points in the Youtube conversation that make it clear what's going on in the Verison employees' heads.
- Both supervisors would agree that 1 cent was different from 1 dollar, and that 0.5 cents was different from 0.5 dollars, but would deny that 0.002 cents was different from 0.002 dollars, explicitly claiming them to be the same quantity.
- When the customer asked the rep to confirm the price, the supervisor would frequently just say "0.002", without seeming to think that the unit was important.
- The customer asks "how do you write down 1 cent", and the supervisor says ".01".
- One of the supervisors said "what do you mean .002 dollars?", "there's no .002 dollars", "I've never heard of .002 dollars", and "you were quoted 0.002 cents; that's 0.002."
What seems to have happened is that none of these reps actually understand what a dollar or a cent are. Rather, they've learned a heuristic of "if the number is big I should describe it with the word 'dollars', and if the number is small I should describe it with the word 'cents'". For numbers in between they'd sometimes be able to do math properly, but for a number as small as 0.002 the rep would hear "0.002 dollars" and think to themselves "small number therefore cents", disregarding the fact that it said "dollars". This is how you get things like the rep saying "our price is 0.002 cents per kilobyte, and you used 35,893 kilobytes, so multiplying those numbers together on my calculator gives me 71.786 dollars". The result on their calculator was bigger than 1, so they ignored the fact that they had originally been working in cents, simply thinking "big number therefore dollars".
Understanding what a unit is would have helped here too. These reps were treating dollars and cents as being redundant descriptive qualifiers added to a number. If a store is 1 mile away from me, I could describe it as "1 mile away", but I could also say "it's only 1 mile away". The "only" serves to highlight the smallness of 1, but doesn't add any other information. The reps were acting as though saying "cents" were simply a way to highlight that a number is small, rather than actually defining what that number is counting.
Yes, most people are incompetent at basic arithmetic