An Actually Correct Explanation of P-Values

It's become a running joke that nobody understands p-values. 46% of Ob-Gyn doctors incorrectly answer a simple question about what p-values are. 89% of "Introduction to Psychology" textbooks that cover statistical significance do so incorrectly. When some doctors did a survey of medical residents to see how many of them understood p-values, none of the possible answers on the survey were correct. FiveThirtyEight writes about how not even scientists can easily explain p-values. While writing this article, I Googled "an intuitive explanation of p-values" and read the first 20 results. 16 of them contained statistical errors.

I recognize the danger of trying to write my own guide. Many of the p-value explanations referenced above did something very similar; start by saying that p-values are often misunderstood, claim they're providing a better answer, then make a bunch of embarrassing mistakes. The risk of me doing the same is, to some extent, unavoidable, but I've done my best. If you notice any mistakes or omissions, please contact me. (I generally correct errors in my articles within a few hours of being notified of them.) Given this, and in accordance with Cunningham's Law I will now state that this is the definitive introduction to p-values.I'm sure there are many textbooks that do a better job of explaining the details for those going into professional statistics. I only aim for this to be a guide for intelligent laypeople.

So what is a p-value? The technical definition:

The p-value of a study is an approximation of the a priori probability that the study would get results at least as confirmatory of the alternative hypothesis as the results they actually got, conditional on the null hypothesis being true and there being no methodological issues in the study.

"A priori" means that we're looking at the probability that would have been calculated before the study took place. (After the study is conducted, the probability is always 100%; those results were in fact gotten!) "Null hypothesis" refers to the hypothesis that whatever effect being tested for doesn't exist. For example if you want to know whether a certain drug cures malaria, the null hypothesis would be "this drug has no effect on malaria". The alternative hypothesis is the one that they're testing for, like "this drug does cure malaria". And "confirmatory results" are any results that would indicate your alternative hypothesis is true. If you're testing to see whether a drug cures malaria, an example confirmatory result would be that 95% of people you give the drug to are cured within a day.

So in other words, if we assume that whatever effect is being tested for doesn't exist, the p-value is a rough measure of the chance that you'd get results that look at least this promising just due to random chance.

Orin even simpler terms, the p-value is a measure of how surprised you should be by seeing these results, if you thought that the effect being tested for didn't exist.

Let's break that down a little more.

Conditional probability

You've built a die-rolling machine, and you want to get a 5. You have two dice available to you: a d6 and a d20. Which should you put in the machine?

To make your decision, you'd want consider what the probability would be of getting a 1 if you made either choice. if you were to choose the d6, your chance of rolling a 5 is 1/6. This is the conditional probability of rolling a 5, conditional on choosing the d6. The probability of rolling a 5 conditional on choosing the d20 is only 1/20, which is lower than 1/6, so you should choose the d6.

(There's also some unconditional probability of rolling a 5, which depends on all of your knowledge about the situation. For example if you know that your friend has already loaded a die into the machine and flipped a coin in order to decide which die to put in, then the unconditional chance of rolling a 5 would be (1/6 * 1/2) + (1/20 * 1/2).)

The unconditional probability of a certain event is generally written as P(event), and the conditional probability as P(event|condition). The "|" symbol can be read as "conditional on" or "given", so P(falling|climbing the ladder) means "the chance of falling conditional on climbing the ladder". If you don't climb the ladder, the chance would be lower.

The most important thing to understand about conditional probability is that P(A|B) does not necessarily equal P(B|A). If all you know about Alice is that she went swimming, what's the chance that she got wet? Extremely high! But if all you know about Alice is that she got wet, what's the chance she went swimming? Much lower; it could have been rain, or a sprinkler, or taking a shower, or any number of other causes.If you're unfamiliar with using probabilities for complicated real-world events like this, see my intro to subjective probability.

This is one of the most common errors made with regards to p-values: the p-value tells us P(data|null hypothesis), but the quantity we actually want to know is P(null hypothesis|data). These are not the same!

Let's say you want to test the hypothesis that wearing a green hat makes any die you roll get its max result. You put on a green hat and roll a d20, and it comes up 20. If the null hypothesis were true (the null hypothesis being "the hat has no effect on the die"), the chance of getting such a good roll would be only 1/20, or 5%. So the p-value of this experiment is 0.05.

Does this mean you can conclude that the null hypothesis has only a 5% chance of being true, and it's 95% likely that wearing a green hat does affect die rolls? Of course not! We have centuries of investigation by mathematicians, physicists, and superstitious D&D players into how dice work, and we can be extremely confident that the color of hat you're wearing has no measurable influence on the result. P(data|null hypothesis) in this case is 0.05, but P(null hypothesis|data) is more like 0.9999999.

Confusion abounds

False statements like "the p-value is the chance that the null hypothesis is true" are extremely common in casual and professional teaching resources alike. One study found that 63% of evolutionary biology papers that found a nonsignificant p-value falsely reported this as their tested effect not existing.

Even when a resource manages to avoid saying that explicitly, that assumption often sneaks in elsewhere. You'll see stuff like "if the p-value is low, you can be confident that the effect you're testing for probably exists", or "the p-value is a way of quantifying how confident we should be that the null hypothesis is false". These are all the exact same error, just stated in different words.Some resources even include an explicit disclaimer that the p-value does not equal the probability the null hypothesis is true, explain that this is a common misconception, and then go on to implicitly rely on it themselves later in the text.

Why does it happen so frequently? Well, because that's what we intuitively want from a study. When we perform an experiment, the purpose is to figure out whether some effect exists, with the idea being that we gather data and check if the data supports the hypothesis. So what we want to find out is P(hypothesis|data), but what p-values actually tell us is P(data|hypothesis), which could be wildly different.

Indeed, even the traditional terminology of "rejecting the null hypothesis" is highly misleading. If you ask a statistician, they'll tell you that "rejecting the null hypothesis" is just a synonym for "p was less than 0.05". But in normal English, "rejecting" a statement kind of implies that you don't think it's true. As we saw with the green hat example, it does not work this way; you could run an experiment rolling a few dice, "reject the null hypothesis", and still justifiability be extremely confident that wearing a green hat had no effect on the dice you rolled.

This is the cause of all of the confusion I mentioned in the first paragraph. p-values are what the entire field of null hypothesis significance testing is built uponIn traditional scientific publishing, you can only publish if you get a p-value of 0.05 or lower. Any higher is seen as a "failure"., but they don't actually mean what most people think they mean.

So why do we use them?

In the D&D video above, the players roll sixteen 1s in a row, equivalent to a p-value of ~0.0000000000000000000015. In such a situation, should we still conclude that the dice are fair? No. That's such an unlikely occurrence that we should clearly start to think something else is going on.In this case, a staged video. But it could also be something within the frame of the experiment, like weighted dice.

We don't always need such a low p-value in order to draw a conclusion about the probability of the null hypothesis. Maybe you want to investigate whether ants like peanut butter. Ants don't eat most substances, so you start with the null hypothesis that ants don't care about peanut butter. You run a test that counts the number of ants that go towards different things, and find that they spend a lot more time near the peanut butter than near a rock, with a p-value of 0.04. Here we can reasonably conclude that ants do like peanut butter even without a particularly low p-value.

The difference has to do with our existing beliefs about the situation. We already know that dice are not affected by a green hat, so a huge amount of evidence is needed to overcome that. Whereas ants liking peanut butter is very plausible given what we already know about ants, so much less evidence is needed in order to conclude that it's probably true.

So a p-value alone does not tell us the chance that the null hypothesis is true, but when combined with our prior beliefs about the world, it can. This is formalized in Bayes' Theorem: P(H|E) = (P(H) * P(E|H)) / ((P(H) * P(E|H)) + ((1 - P(H)) * P(E|¬H))).For an intuitive guide to Bayes' Theorem, see Arbital, 3Blue1Brown, or Rational Animations. ("H" stands for the null hypothesis, and "E" stands for the evidence we acquired.)

That is, we start with our prior belief about how likely it is that ants don't like peanut butter, before looking at any of our experimental data. Let's say it's 50%, since we know that ants like some human food, but not all of it, and we have no idea how they'll feel about peanut butter. That's P(H). (Remember that we're testing the null hypothesis here, not the alternative hypothesis.) P(E|H) is our p-value, the chance of observing evidence at least this strong given that the null hypothesis is true, which our experiment determined is 0.04.Ideally with Bayes' theorem you'd use the probability of observing only the exact evidence you did observe, not also the chance of having seen even stronger evidence. So plugging p-values into Bayes' Theorem is unnecessarily discarding some information and will make your inference less powerful, but the theoretical idea is the same either way. We also need P(E|¬H), which is the chance that we'd get evidence at least this strong given that the null hypothesis is not true. We can call that 99%, since we're pretty sure that we designed a good experiment; if ants do like peanut butter, they'd almost certainly go towards it in our setup. Plugging in all the numbers gives us a final result of only ~4% likelihood that the null hypothesis is correct; ants probably do like peanut butter.

Doing this in the die rolling example gives us a different result. Our prior belief that green hats do not influence die rolls is 0.9999999, we think that if green hats do influence die rolls there's a 99% chance the die will come up 20 while we're wearing the hat, and we performed the experiment and got a p-value of 0.05. Using Bayes' theorem, we get out a posterior probability of 0.99999802 for the null hypothesis. Seeing the die come up 20 while wearing a green hat has slightly decreased our confidence that the die is fair, but not by much.

So p-values are useful! But only with the context of our existing knowledge about the world.

Practical significance

So the p-value on its own does not tell you the chance that the paper is wrong. However, it can be used to derive the false positive rate. Traditional statistical significance testing has you choose a specific number, called alpha, and if your p-value is less than or equal to alpha, you "reject the null hypothesis" and can publish your paper. Alpha is usually set to 0.05. This means that, if we assume no experimental error, out of 100 papers investigating a true null hypothesis, we'd expect 5 (on average) to get a p-value of 0.05 or below and incorrectly reject the null hypothesis.

(For studies where the null hypothesis is true, the p-value varies randomly.Only true for most tests, like T-tests and Chi-squared tests. It's not true for other types, like logistic regression. You have an equal chance of getting any p-value from 0 to 1. So the chance of getting a p-value that's <= X is just X.)

But knowing that the false positive rate is only 5% can be deceptive. The false positive rate is not the chance that a given study is wrong due to having a false positive, nor is it the chance that a study that found a positive result is wrong.Both of these are extremely common misconceptions. I polled my followers on Twitter, who are much more statistically literate than the average person, and more than 90% of the ones who thought they knew the answer gave one of those two incorrect definitions.Despite already knowing how frequent this point of confusion is, when I first programmed this widget, I did so using a wrong definition of the false positive rate, then spent a while confused about why its results made no sense before I looked up the correct definition and realized my error. It is the chance that a study that was investigating an effect that doesn't exist comes up positive just by chance. (Note how this is just the definition of a p-value.) Since the whole problem is that we don't know whether the effect exists in the first place, the false positive rate on its own isn't all that useful.

I've created a simple demonstration of this. In addition to choosing the p-value threshold (alpha), you'll also need to choose the average study statistical power, which is how well the study would successfully detect an effect that does exist. And you'll need to pick the overall prevalence of studies that are investigating an effect that actually exists. Those three factors determine the outcome of any study performed."For a handy guide to all these terms: statistical power, specificity, false positive rate, likelihood ratio, etc., see Wikipedia's aptly-named table of confusion.

(Note how these correspond exactly to the inputs of Bayes' Theorem. The p-value is P(E|H), the statistical power is P(E|¬H), and the prevalence is the prior, P(H).)

Once you've chosen those three factors for a scientific field, the colored area on the right shows a breakdown of what all the studies would be like in that field. You can think of each pixel as a single study, so the area of a certain color is proportional to the fraction of studies in the field that had that result.If you're curious how it's calculated: the alpha level is the chance that a study that's investigating a true null hypothesis gets a false positive, so it's the ratio of the red area to the red + blue areas. The statistical power is the chance that a study investigating a false null hypothesis, gets a true positive, so it's the ratio of the green area to the green + pink areas. And the prevalence is the total number of studies that are investigating a false null hypothesis, so it's the ratio of the green + pink areas to the whole square. Once you have those three ratios, it's just some very simple algebra to calculate what fraction each area takes up.

Alpha:
Average statistical power:
Prevalence:

Consider a realistic example from psychology. Set the alpha level to 5% and the statistical power to 80%, which are the traditional target values for each. Psychology tends to investigate some... questionable ideas, so let's say that 10% of studies are investigating a real effect.

We see that 93.5% of studies will be correct, which seems pretty good at first glance. +But the vast majority of those correct results are true negatives, and any study that came up negative, finding no effect, likely won't be published. If we look only at the positive studies, a full 36% of them are wrong! That's not great.

This is what's going on in the classic XKCD comic:

The p-value is working exactly as intended here. They performed 20 studies, got 19 true negatives and 1 false positive for a false positive rate of 5%, as expected. But only the positive one is exciting enough to get published or mentioned in the news, so the wrong result ends up being much more impactful than the correct ones.

It gets worse. 80% statistical power may be recommended, but it's usually not reached. Estimates of the actual power in most studies range from less than 50% in psychology and around 20% in neuroscience, to 7% in economics, to less than 6% across the board by some of the more cynical statisticians.

And a p-value of <0.05 is also optimistic. Recall that the p-value is conditional on no experimental error. But when a low p-value makes it easier to publish and gain prestige in the scientific field, there's a lot of incentive for convenient errors. (Note that under the above assumptions, the chance of a paper coming up with a positive result is only 12.5%, meaning researchers are going to have to throw out 7 out of every 8 studies they perform for being nonsignificant. Do you really think they're doing that?FiveThirtyEight has a wonderful interactive simulation of how easy it is to manipulate data until you find a significant result.Note that this form of p-hacking, known as multiple comparisons, data dredging or the look-elsewhere effect, is actually not "experimental error" as far as the philosophical interpretation of p-values is concerned. Rather it's a form of publication bias. Each particular way of analyzing data is effectively its own study, and the researcher can discard thousands of those "mini-studies" before finding one that meets the statistical significance threshold. But there are also other ways to screw up a study that are actual error in the study methodology itself.)

If you change the simulation above to use more realistic values of alpha = 10% and power = 20%, now more than 80% of published studies are wrong. And indeed, the fact that most published research is false is well-accepted.

As you can see in the simulation, a low p-value does have a positive effect; the lower you set the alpha, the more reliable the results are. This paper tested this in practice by attempting to replicate 100 published psychology papers, and found that those published with a p-value from 0.04 to 0.06 replicated only 18% of the time, whereas those with p < 0.02 replicated 41% of the time, and p < 0.001 replicated 63% of the time."Replicated" here means that the second study got p < 0.05, not that it got as low as the original study. See also here and here for similar results.

So a low p-value threshold does help improve study accuracy. But... not by that much. In any realistic field of science, a paper with p = X will have a much greater than X chance of being wrong, and you have to take other factors into account in order to correctly derive the practical implications of the study. And if the p-value seems too good to be true... it probably is.

Update: we have a new winner. P = 4.4 * 10^-25121 🤯

From https://t.co/xZsYFxQDi3. Found by @CasualVariant. [4/3] pic.twitter.com/pChLhSLAyG

— Dmitry Kobak (@hippopedoid) June 28, 2023

Are they "evidence"?

A p-value may not be the chance that the null hypothesis is true, but a low p-value still indicates that the null hypothesis is less likely than it would have been if you had gotten a higher p-value, right? So a p-value is a measure of evidence against the null hypothesis, and the lower the p-value is, the more evidence you have against it?

Not exactly. Consider spinning a wheel, and you want to determine if there's a bias in how it will stop. Your null hypothesis is that there's no bias, and your alternative hypothesis is that it is biased towards some area. The only data you have access to is to define a region on the wheel centered where you think the bias might be, and know whether the wheel stopped within that region.

So you start by designating a region equal to 1/100 of the wheel, and it stops inside that region. Your p-value is therefore 0.01. But the amount of evidence that this p-value provides depends on what the proposed bias is! If the bias is narrow, being extremely likely to stop within that region, then this is pretty compelling; it's much more likely that the wheel is biased than that you just got lucky with an unbiased wheel.

But if the bias is broad, causing the wheel to be only slightly more likely to end in that region, then this is quite a coincidence either way. You'd need a lot more spins to begin to get an idea of which hypothesis is more likely.

So a p-value of 0.01 clearly doesn't stand for any constant amount of evidence. Rather what provides the evidence is the ratio between the p-value and the chance of getting data at least this extreme conditional on null hypothesis being false. This quantity doesn't have a name in traditional statistics, so I'll call it the q-value.

(The q-value is related to the p-value in almost the same way that statistical power is related to alpha, just inverted. Alpha determines the false positive rate, and is an arbitrary threshold that the researcher sets in order to classify possible p-values into two buckets of rejecting or not rejecting the null hypothesis. Statistical power is the true positive rate, and could be used as an arbitrary threshold to accept the alternative hypothesis if the q-value falls above it. In practice people generally frame everything in terms of the p-value instead of the q-value, but both framings are functionally equivalent.)

This makes intuitive sense. We're trying to distinguish between possible worlds, so we need to know which world would be more likely to generate the evidence that we've seen. If one of those worlds is much more likely to give us that evidence, then we're probably living in that world. But if the evidence we've observed is largely unrelated to the difference between those possible worlds, and then it doesn't give us much information either way.

We can see this ratio in Bayes' theorem:

So the p-value on its own is not enough to be useful. We also have to know the q-value, and it's the ratio of the two (combined with our prior) that tells us how much we should believe in the null or alternative hypothesis. If the p-value is smaller than the q-value, this is evidence towards the alternative hypothesis. If the q-value is smaller, that's evidence towards the null hypothesis. This is known as the likelihood ratio or Bayes Factor, and it is a measure of evidence.

Now it is true that, if you hold the q-value constant, decreasing the p-value decreases the probability of the null hypothesis. So you could say "all else being equal, a lower p-value is more evidence against the null hypothesis". But the problem with that is that most of the study parameters that are easy to tweak will end up changing not only the p-value but also the q-value. (e.g. making the size of the test area on the spinning wheel smaller makes the p-value smaller, but also makes the q-value smaller.)

Calculating p-values

Ok, enough about the theory. How do scientists actually arrive at their numbers?

First you have to define a clearly-specified null hypothesis. This is usually pretty straightforward, but not always.

Imagine you've developed a new drug called Tybuprofen, and you want to see whether it works as a painkiller. So you gather 100 people experiencing pain, ask them to rate it on a 0-10 scale, give them Tybuprofen, ask them to rate their pain on the same scale again an hour later, and calculate the p-value of the difference. It's 0.001. You can publish!

Then you hear about something called "regression to the mean" and decide to run another study with a control group. You divide your pain-experiencing subjects into two groups at random, one group takes Tybuprofen, the other takes nothing, and you ask them both to rate their pain on the scale. Checking the p-value of the difference, it's 0.02. You can still publish, nice.

But before you can do so, an annoying colleague points out something called the "placebo effect". So you run a third study, this time giving the control group a sugar pill that looks and tastes the same. p = 0.05. Well, it's on the edge of significance, should be fine.

Hmm, but was that the best dosage? Maybe a higher dose would do a better job? You once again gather those who suffer, giving one group 400mg and the other 800mg. Checking the p-value of the resulting ratings, it's 0.11, not significant. Ah well.

You have now run four studies with four different null hypotheses.

• Null hypothesis #1: People on Tybuprofen will experience no reduction in pain.
• Null hypothesis #2: People on Tybuprofen will experience the same reduction in pain as people not on any drug.
• Null hypothesis #3: People on Tybuprofen will experience the same reduction in pain as people on a sugar pill.
• Null hypothesis #4: People on 800mg of Tybuprofen will experience the same reduction in pain as people on 400mg of Tybuprofen.

Each of them was a reasonable choice. But who chooses what counts as "reasonable"? After all, if you were trying to test for the existence of the placebo effect, you'd want to use #2, but if trying to test for a painkiller effect of Tybuprofen in particular, #3 is more fitting. It's context-dependent! And we only want to use null hypothesis #3 because we think the placebo effect exists. We don't feel a need to ensure that our control group is standing at the exact same longitude as the test group, because our model of the world tells us that it's very unlikely for this to have an effect.

Consistently-used null hypotheses, like "people taking the drug report the same outcomes as people on a sugar pill" help cut down on inconsistency when applied across the entire scientific industry. They make sure everyone is on the same page with regards to what, exactly, the p-value is comparing a study's results to. But the choice of null hypothesis that we use to calculate the p-value is somewhat subjective. We try to pick one that is conceptually as "simple" or "boring" as possible, one that doesn't make any assumptions about the world, but we have to be careful, and be clear what we mean when we talk about the null hypothesis.

Ok, now imagine you have a coin that may be biased towards heads or tails. you don't know, but you want to find out. So you flip it 100 times, and get 60 heads. Using the null hypothesis of it being a fair coin, you use a binomial distribution calculator to check the chance of getting ≥60 heads under the null hypothesis that the coin is fair, and get 0.028. So that's our p-value, right?

But wait! That's the chance of getting at least that many heads. What about tails? The coin could have been biased towards tails too. Taking that into account doubles the p-value to ~0.056.

So it matters what hypothesis we're testing, since that determines what "at least as confirmatory" actually means. If the hypothesis is "it's biased towards heads", we only want to check how "extreme" the coin is in the direction of heads. But if the hypothesis is just "it's biased in some way", you'd want to check both directions.

These are known as one-tailed and two-tailed tests, respectively. Consider how likely each number of heads is under the null hypothesis. 50 is the most likely number, then 49 and 51 are next most likely, etc. If you plot these out, you get a binomial distribution.The picture below is actually a normal distribution, because I was lazy and just grabbed it from Wikipedia. It's the same idea either way. The total probability of getting at least N heads is equal to the area under the curve starting at N and going to the right. In the image below, the yellow areas represent a two-tailed test, and a one-tailed test would just be one of the yellow areas. So computing your p-value is just taking the appropriate area under the distribution curve.

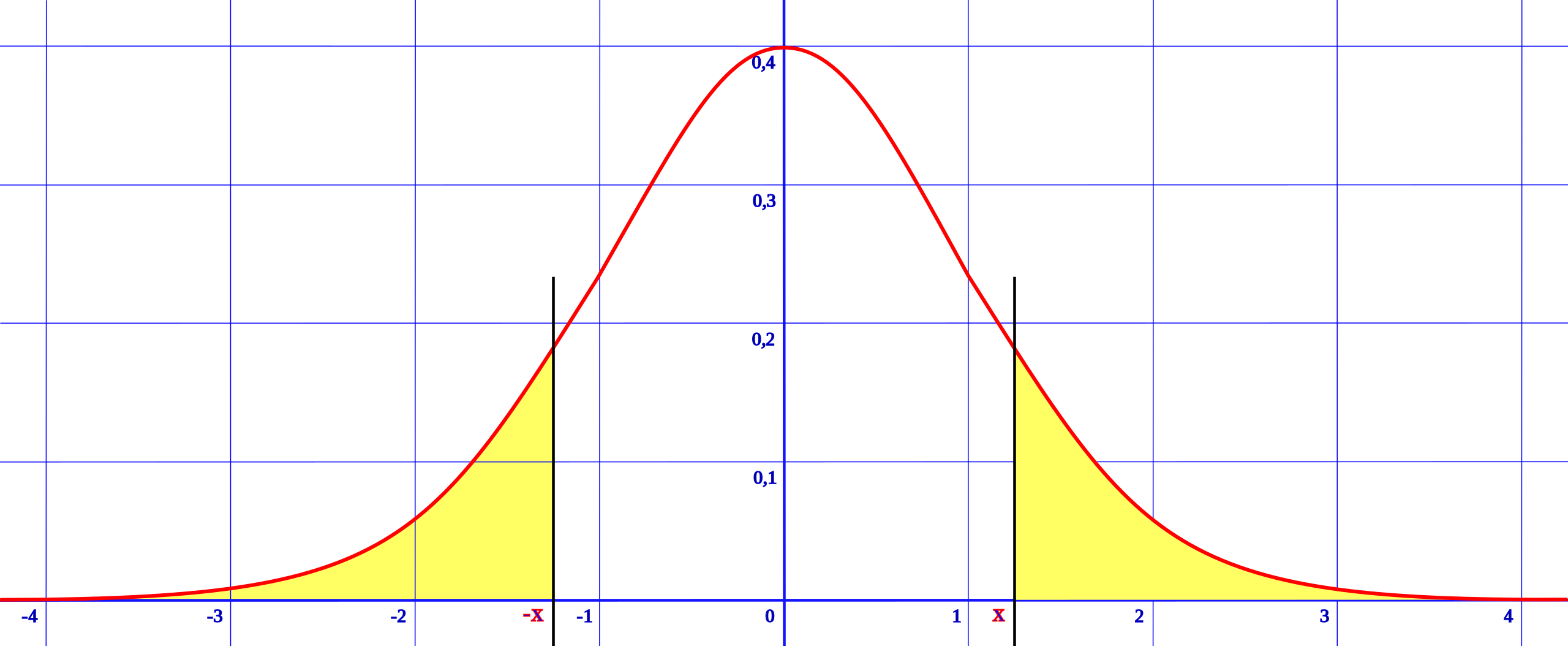
But hold on a minute. "Biased towards heads" isn't a single theory; how biased are we talking?. A coin could be highly biased, getting 90% heads. Or it could be only slightly biased, getting 55% heads. If our p-value is supposed to take into account the alternative hypothesis as well as the null hypothesis, shouldn't we get a different value depending on which specific level of bias is hypothesized? Getting 60 heads out of 100 flips is pretty likely under the theory that the coin is 55% biased towards heads, but very unlikely if it's 90% biased.

And what about more complicated patterns? If you flip the coin 100 times and get 50 heads in a row followed by 50 tails in a row, that doesn't seem very random, but any method of calculating a p-value that relies on only the number of heads (and not their order) will return a high p-value.

There are many different ways to deal with this problem, and this is another source of subjectivity. Different statistical tests are available for different kinds of hypothesis; one and two tailed tests, Student's t-tests, F-tests, chi-squared tests, one-way ANOVA, etc. The experimenter has to choose which one makes the most sense for their particular hypothesis.

Most significance tests rely on collapsing the data down to a single number, called a "test statistic", and then comparing that number to the distribution of numbers you would expect to get under the null hypothesis. In our first coin flip example, the total number of heads was the test statistic, and the p-value is a measure of how far away from the mean of the binomial distribution it lies.

This is why I said at the beginning that the p-value is more of an approximation. When a scientist comes up with a hypothesis like "Tybuprofen reduces pain", that really stands for an infinite class of hypotheses that each have it reduce pain by a different amount. The scientist picks some formalization of this hypothesis that puts a specific probability distribution over the outcomes, then picks some way to compare that distribution to the null hypothesis distribution, and reports that as the p-value. (Or in simple cases like the coin flip example, they just look at the distance from the mean of the null hypothesis, without needing a specific alternative distribution.) So different reported p-values are testing subtly different things, depending on the particular test used.

Test yourself

To help you make sure you understand p-values correctly, I've taken some quotes about p-values from various scientists and statisticians, and you can grade them as right or wrong.

#1. From Choosing and Using Statistics: A Biologist's Guide (second edition), a textbook from 2009, written by a professor of biology at the University of York:

"The P-value is the bottom line of most statistical tests. It is simply the probability that the hypothesis being tested is true. So if a P-value is given as 0.06, that indicates that the hypothesis has a 6% chance of being true. In biology it is usual to take a value of 0.05 or 5% as the critical level for the rejection of a hypothesis. This means that providing a hypothesis has a less than one in 20 chance of being true, we reject it. As it is the null hypothesis that is nearly always being tested we are always looking for low P-values to reject this hypothesis and accept the more interesting alternative hypothesis."

Is this statement correct?

Show answer

#2. From Choosing and Using Statistics: A Biologist's Guide (third edition), the same textbook from 2011:

"The P-value is the bottom line of most statistical tests. It is the probability of seeing data this extreme or more extreme if the null hypothesis is true. So if a P-value is given as 0.06 it indicates that you have a 6% chance of seeing data like this if the null hypothesis is true. In biology it is usual to take a value of 0.05 or 5% as the critical level for the rejection of a hypothesis. This means that providing a hypothesis has a less than one in 20 chance of being true we reject it. As it is the null hypothesis that is nearly always being tested we are always looking for low P-values to reject this hypothesis and accept the more interesting alternative hypothesis."

Is this statement correct?

Show answer

#3. From Stevenson, 2024; a review of methodological errors in criminology research and how the replication crisis has affected the field:

"With standard hypothesis testing methods, there will be one false claim of a relationship between a cause and purported effect for every nineteen times that it fails to find support"

Is this statement correct?

Show answer

#4. From Davis & Mukamal, 2006; a statistical primer for cardiovascular research:

"For hypothesis testing, the investigator sets the burden by selecting the level of significance for the test, which is the probability of rejecting the null hypothesis when the null hypothesis is true."

Is this statement correct?

Show answer

#5. From the Towards Data Science blog with several hundred thousand readers, written by Cassie Kozyrkov, former chief decision scientist at Google:

"All of hypothesis testing is all about asking: does our evidence make the null hypothesis look ridiculous? Rejecting the null hypothesis means we learned something and we should change our minds. Not rejecting the null means we learned nothing interesting, just like going for a hike in the woods and seeing no humans doesn’t prove that there are no humans on the planet. It just means we didn’t learn anything interesting about humans existing."

Is this statement correct?

Show answer

#6. From a speech at the Royal Statistical Society by Sir David Cox, winner of the 2017 International Prize in Statistics:

"If we found a p-value of 7%, it would say 'if we were to take these data as just decisive against the null hypothesis, then in 7% of the cases in the long run in which the hypothesis is true, it will get rejected falsely'."

Is this statement correct?

Show answer

#7. From ChatGPT when I asked it what a p-value is:

"A p-value quantifies the strength of evidence against the null hypothesis. By comparing the p-value to a predetermined significance level (usually 0.05), researchers can assess the likelihood that their observed data would occur if the null hypothesis were correct. A small p-value suggests that such data are unlikely, indicating strong evidence against the null hypothesis."

Is this statement correct?

Show answer

#8. From Elementary Statistics in Social Research, a textbook by James Alan Fox and Jack Levin, both well-known criminologists who frequently consult for the white house and in criminal trials:

"The difference between P and a can be a bit confusing. To avoid confusion, let’s compare the two quantities directly. Put simply, P is the exact probability that the null hypothesis is true in light of the sample data; the a value is the threshold below which is considered so small that we decide to reject the null hypothesis. That is, we reject the null hypothesis if the P value is less than the a value and otherwise retain it."

Is this statement correct?

Show answer

#9. From the Simple English Wikipedia's February 2021 page on misuse of p-values:

"In statistics, a p-value is the probability that the null hypothesis (the idea that a theory being tested is false) gives for a specific experimental result to happen. p-value is also called probability value. If the p-value is low, the null hypothesis is unlikely, and the experiment has statistical significance as evidence for a different theory."

Is this statement correct?

Show answer

#10. From Kareem Carr, Twitter statistician:

"THE LOGIC OF THE P-VALUE. Assume my theory is false. The probability of getting extreme results should be very small but I got an extreme result in my experiment. Therefore, I conclude that this is strong evidence that my theory is true. That's the logic of the p-value."

Is this statement correct?

Show answer

#11. From a review of common p-value misinterpretations:

"Any P value less than 1 implies that the null hypothesis is not the hypothesis most compatible with the data, because any other hypothesis with a larger P value would be even more compatible with the data."

Is this statement correct?

Show answer

#12. From the Firebase A/B test documentation:

"P-value, which represents the probability that there is no true difference between the variant and baseline; in other words, any observed difference is likely due to random chance. The lower the p-value, the higher the confidence that the observed performance remains true in the future."

Is this statement correct?

Show answer

With thanks to VesselOfSpirit, detectiveenters, and Tom Kealy for feedback and suggestions. Any errors are my own.

Outside the Asylum

Subscribe

RSS feed